QDrop

QDrop是发表在ICLR2022的一篇文章，而且评分达到了前1%，是一种可以在量化中加插即用的算法。在读这篇文章之前，读者最好了解一些在它发表之前的前瞻工作，如： AdaRound、BRECQ等，以及一些关于优化理论的概念，如：Hessian矩阵、FIM、flat minima。具体的一些联系如下面的思维导图所示。

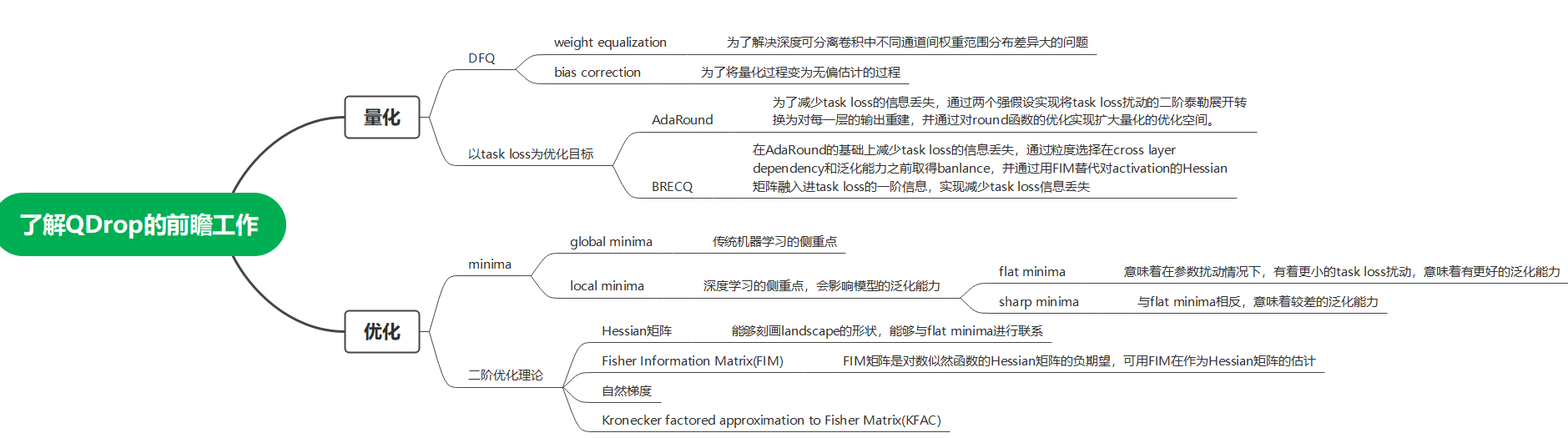
图 0.1： QDrop相关概念的思维导图

量化的过程可以看作是对原始的模型添加扰动噪声，量化的目标是在在对原始模型添加扰动的前提下，使得扰动后的模型保持量化前的性能（泛化性角度来说就是具有更强的泛化能力）。在早期，传统量化网络都是从参数空间进行优化，最小化量化前与量化后的参数误差，而这种优化目标显然是不合理的，最小化参数误差并不一定会使网络的输出误差最小。而AdaRound和BRECQ是从model space进行优化的，它们的优化函数都是task loss的误差，QDrop也是在优化task loss的前提下开展的。

在BRECQ的总结文档里说过，当前离线量化PTQ工作的两个难点是：

1. loss信息，并使其降低；

2. 如何用有限的数据集在短时间内校准出一个量化模型。

AdaRound和BRECQ都是在解决第(1)点问题。AdaRound其实是一篇里程碑式的文章，它创新的扩大了优化空间，将原始的优化参数由2(S、Z)扩大到了N*C*W*H，将优化参数扩展为round函数，只不过在它的公式推演中用了过强的假设条件，丢失了很多的task loss信息。而BRECQ是在AdaRound的基础上，进一步增加task loss信息，通过对cross layer dependency的分析成功的将优化粒度由layer扩展到block，在求task loss对pre-activation的Hessian矩阵用FIM来代替，融入了一阶导数信息，从而减少了task loss信息的丢失。但是在这里并没有明确的对block的定义，对粒度的划分也比较粗略。

本文QDrop是在解决第(2)点问题。在PTQ工作中，实践告诉我们validation set的选取是十分重要的，PTQ对validation set也是十分敏感的，这也侧面反映了量化后模型的泛化能力的重要性。QDrop通过对activation扰动转化为等效的weight扰动的分析来引入flatness，并随机丢弃activation实现了多方向探索flat minima，从而增强模型的泛化能力，利用有限的validation set的校正在test set上实现良好的效果，这就是QDrop的核心。

下面依然从动机、实现技巧、实验现象和总结(本质)几个方面对QDrop进行理论上和实践上的分析。

1. 动机

在之前的量化工作中，例如AdaRound、BRECQ等，通常忽视activation的量化，或者是将weight统一量化完成后在进行activation量化，这就使得activation的2bit量化模型和4bit的量化模型具有相同weight模型。而直觉上讲，使得activation的2bit、4bit的量化模型发挥最好作用的weight应该是不同的。所以QDrop的研究目的或者说动机就是，在量化weight的过程中考虑由于activation的量化带来的误差而对weight量化带来的影响，本质上来讲就是将activation量化和weight量化一起来做。

通常上来讲，在分析两个事情同时变化的时候就会出现一个问题，两个东西一起做就会出现两个浮动的事情，不好把控，一般的做法是以其中一个事物作为锚点，相当于参考系，另一个事务以锚点的视角进行描述。AdaRound就是这种思想，其是以weight量化作为锚点，将activation量化看作weight量化的一种噪声来进行分析。

2. 实现技巧

2.1 实验上的观测

为了验证自己的动机是否正确，作者做了三个小实验互相形成对比。

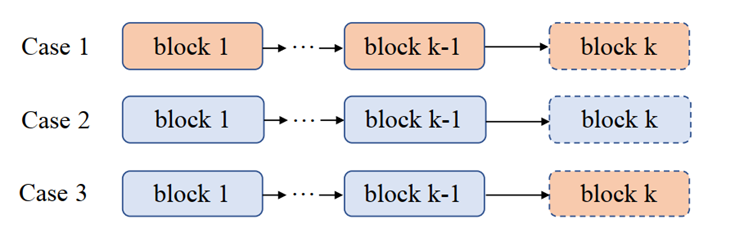
图 2.1： 3组toy_example对比实验

如图2.1所示，在Case1中，作者在对第k个Block的weight量化时，并没有考虑前k-1个Block的activation的影响，这就和之前的AdaRound、BRECQ等的方式一致。在Case2中，作者在对k个Block的weight量化时，考虑前k个Block的activation量化的影响，这就导致第k个weight的量化感受到了所有activation的量化噪声。在Case3中，作者在对k个Block的weight量化时，考虑前k-1个Block的activation量化的影响，Case2和Case3相比，Case3忽视了第k个Block的activation量化的影响。 直觉上来讲，在ImageNet上W2A2的准确率应该是Case1<Case3<Case2。而实际的结果图如图2.2所示。

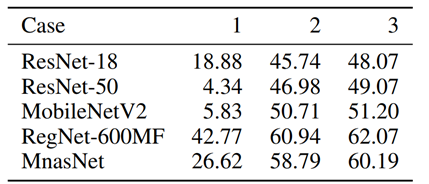
图 2.2： toy_example的实验结果图

结果表明，在不同的backbone上，准确率均为Case1<Case2<Case3。Case1和Case2对比表明，在低bit(2bit)的情况下，考虑activation量化会给结果带来很大的提升，在MobileNetV2上涨点接近45%。因此这也表明，分开考虑weight和activation的量化不利于在低bit上量化，在量化activation之后量化weight有助于weight学习消除由activation量化带来的扰动噪声，从实践上初步验证了第一小节动机的成立。而直觉上Case2的准确率应该高于Case3，但实际上却相反，这启发作者部分引入activation的量化的结果要好于引入全部的activation量化。

2.2 对activation的扰动转化成等效的weight扰动分析

实验验证了activation和weight联合优化确实有正向作用，按照第1节动机中的内容，想要分析二者的关系，需要给定锚点，另一个事务以锚点的视角进行描述。AdaRound是以weight量化作为锚点，将activation量化看作weight量化的一种噪声来进行分析。本小节从数学推导出发定量的研究如何联动二者。

把由于activation量化带了的扰动噪声定义为：

$$\tag{2.1} e = \hat{a} - a$$

(2.1) 中噪声为线性噪声，此种定义方式有一种明显的缺点：噪声的大小与原始精度 activation 的$a$ 的范围密切相关。如果令由 $\text{round}$ 带来的误差为 $c$ 的话，$c \sim U[-0.5, 0.5]$，则在 (2.1) 的定义下，有：

$$\begin{aligned} \tag{2.2} e &= \hat{a} - a \\ &= \left( \text{round}\left(\frac{a}{s}\right) \cdot s - a \right) \\ &= \left( \text{round}\left(\frac{a}{s}\right) - \frac{a}{s} \right) \cdot s \\ &= c \cdot s \end{aligned}$$

其中，$s$ 代表量化参数 scale，也称为 step size，其大小与量化 bit 和原始 activation 输入范围密切相关。因此，(2.1) 的定义的 $e$ 也会受原始 activation 输入范围大小的影响，在大范围输入时噪声放大。在 activation 范围的情况下，噪声 $e$ 也就会随之变大，这不利于我们用统一的标准分析整网的量化误差。我们需要选择一种与 step size 分离开来的噪声定义方式，乘性噪声：

$$\tag{2.3} e = u \cdot a$$

在 (2.3) 的定义下有：

$$\tag{2.4} \hat{a} = (1 + u) \cdot a$$

因此，

$$\tag{2.5} \begin{aligned} u &= \frac{\hat{a}}{a} - 1 \\ &= \frac{\bar{a} \cdot s}{\left(\overline{a + c}\right) \cdot s} - 1 \\ &= \frac{-c}{a + c} \end{aligned}$$

其中，$\bar{a} = \frac{\hat{a}}{s}$ 是 $a$ 在定点域下对应的数值。因此在 (2.3) 的定义下，噪声大小与 step size 分离开来，方便我们做定量分析。

在优化 task loss 和考虑 activation noise 的前提下，PTQ 的优化目标变为了：

$$\tag{2.6} \arg \min_w \mathbb{E}_{x \sim D_c} \left[L \left(w + \Delta w, x, 1 + u(x) \right) - L(w, x, 1)\right]$$

其中，$x$ 代表的是 Input data，$D_c$ 代表的是 PTQ 的 validation set。

接下来要做的就是定量的将 activation noise 转化为对 weight 的影响，即找到合适的 $V(x)$ 使得：

$$\tag{2.7} W \odot \left(a \odot (1 + u(x))\right) = \left(W \odot (1 + V(x))\right) a$$

其中，$\odot$ 代表 element-wise 乘法。

即：

$$\tag{2.8} W \odot \begin{bmatrix} 1 + u_1(x) & 1 + u_2(x) & \cdots & 1 + u_n(x) \\ 1 + u_1(x) & 1 + u_2(x) & \cdots & 1 + u_n(x) \\ \vdots & \vdots & \ddots & \vdots \\ 1 + u_1(x) & 1 + u_2(x) & \cdots & 1 + u_n(x) \end{bmatrix} = \left(W \odot \begin{bmatrix} 1 + u_1(x) & 1 + u_2(x) & \cdots & 1 + u_n(x) \\ 1 + u_1(x) & 1 + u_2(x) & \cdots & 1 + u_n(x) \\ \vdots & \vdots & \ddots & \vdots \\ 1 + u_1(x) & 1 + u_2(x) & \cdots & 1 + u_n(x) \end{bmatrix} \right)a$$

因此，(2.7) 的解为：

$$\tag{2.9} V_{i,j}(x) = u_j(x)$$

因此，(2.6) 可转化为：

$$\tag{2.10} \begin{aligned} &\arg \min_w \mathbb{E}_{x \sim D_c} \left[L \left(w + \Delta w, x, 1 + u(x) \right) - L(w, x, 1)\right] \\ &\approx \arg \min_w \mathbb{E}_{x \sim D_c} \left[L \left((w + \Delta w) \odot (1 + v(x)), x, 1 \right) - L(w, x, 1)\right] \end{aligned}$$

(2.10) 的含义是：将 activation 的扰动 $1 + u(x)$ 转化为相应的 weight 的扰动 $1 + V(x)$。

---

2.3 对 flatness 的引入与分析

在论文中，作者通过一系列的数学推导，使得 (2.10) 转化为：

$$\tag{2.11} \begin{aligned} &\arg \min_w \mathbb{E}_{x \sim D_c} \left[L \left(w + \Delta w, x, 1 + u(x) \right) - L(w, x, 1)\right] \\ &\approx \arg \min_w \mathbb{E}_{x \sim D_c} \Bigg[ \underbrace{\left(L \left(w + \Delta w, x, 1 \right) - L(w, x, 1)\right)}_{(1)} + \underbrace{\left(L \left((w + \Delta w) \odot (1 + v(x)), x, 1 \right) - L \left(w + \Delta w, x, 1\right)\right)}_{(2)} \Bigg] \end{aligned}$$

其中的$w+\Delta w$就是原论文中的$\hat{w}$，就是反量化后的权重，论文把量化看做了扰动。(2.11)分为两部分，分别为(1)、(2)，(1)其实就是之前的AdaRound和BRECQ等论文的优化目标，即在优化权重时不考虑activation量化带来的影响，优化权重量化前后的损失。(2)式表示了由activation noise引起对应等价的weight部分的扰动。仔细发现(2)其实是在2017年发表的<Exploring Generalization in Deep Learning>论文中对sharpness的定义，作者沿用了该论文中sharpness的定义。

笔者对flatness也有一点研究，在自己的论文中也有体现，哪天有机会可以把论文给大家分析一下。flatness是在loss landscape上的局部空间是平坦的，其可以体现为：对权重施加扰动，如果在扰动下模型的Loss的变化很小则称此优化点在loss landscape下具有较大的flatness。在研究flatness和泛化性的文章中表示，传统机器学习和深度学习在优化这方面有比较大的不同，传统机器学习大家在乎的更多是找到是local minima还是global minima。Local minima意味着train loss还比较高，还没有优化到位；但是在深度学习里，无论是local minima还是global minima对应的loss都差不多小。深度学习中，大家比较在乎的是saddle points(鞍点)附近的动力学，这会影响优化；大家更在乎的是找到的点是flat minima还说sharp minima，这会影响泛化，flat minima意味着在参数空间的扰动下task loss有着小的变动，所以深度学习优化中非常重要的两个核心问题是：

1. 怎样快速逃离鞍点；
2. 怎样逃离sharp minima找到flat minima。

flatness的概念对于泛化能力至关重要，这也是在绪论中所提到PTQ面临的两大问题中的第(2)点如何用有限的数据集在短时间内校准出一个量化模型所提及的关键点。(2.11)的意义在于将量化模型task loss的改变成功的与flatness或者说是泛化能力挂上钩，这是通过将activation的量化视为weight量化的扰动而实现的。这也意味着在重建量化网络中考虑activation noise的话，量化模型的泛化能力会随之提升。用数学定理的形式来阐述上述内容，就是论文中的Corollary 1，在校准数据 上，具有激活量化噪声$u(x)$，存在相应的权重扰动$v(x)$,使得训练的量化模型在扰动$v(x)$下更平坦。

用Corollary 1的内容，也可以更好地解释2.1小节中三个Case的实验结果，Case 1和Case 2在考虑activation noise的情况下，有着更大的flatness，或者说是有着更平坦的局部landscape。

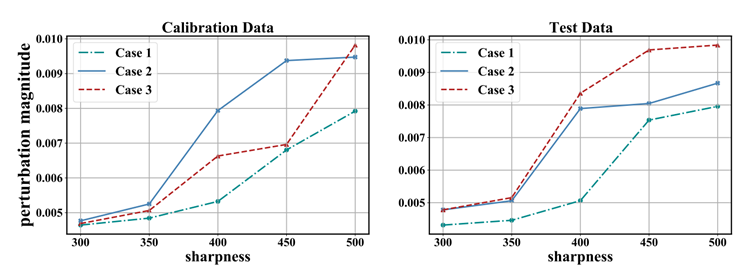
图 2.3： Case中的扰动

图2.3更加直观的展示了Case1、2、3中的sharpness，可以看出，在相同的扰动下，Case 2、3拥有着更小的sharpness，也就是更平坦的landscape，也就会有着更小的loss下降。

2.4 借鉴Dropout的方法实现多方向探索flat minima

由2.3小节内容可知，引入activation量化可以产生比现有模型更平坦的模型，平坦度的方向取决于数据分布，这也说明了PTQ对数据是十分敏感的，并且仅在validation set有更平坦的模型不够，PTQ的最终目标是在test set上有更平坦的模型。

在图 2.3 中可以看出， $v(x)$ 和 $u(x)$ 是会随着 Input data 的改变而变化的。在三个 Case 中，由于对 activation 量化的情况不同，三个 Case 的 $u(x)$ 不同，导致产生了不同的 $V(x)$，在对 flatness 的探索上就会出现了不同的方向选择。

• Case 1:

$$\tag{2.12} u = 0$$

• Case 2:

$$\tag{2.13} u = \hat{a} / a - 1$$

• Case 3:

$$\tag{2.14} u = \begin{cases} \hat{a} / a - 1, & \text{block}_1 \sim \text{block}_{k-1} \\ 0, & \text{block}_k \end{cases}$$

对于Case1，它没有考虑由activation量来带来的影响，也就没有考虑扰动的影响；对于Case2，它考虑了全部的activation noise，因此其在validation set上有着不错的表现，但是因为validation set的数目比较少，其很容易造成过拟合，导致其在test set上表现差；对于Case3，它仅考虑了前k-1个block的activation noise，而忽视了第 个block的activation noise，相对于Case2来说，降低了过拟合，因此，Case3在test set上取得了最好的结果。

上面这段话，启示我们可以从过拟合的角度来思考 activation noise，在降低过拟合方面 dropout 和 Case3 的情况十分类似。这也启示作者可以从随机丢弃部分 activation 来实现降低过拟合的作用。注意，从过拟合角度思考和从 flat minima 角度思考并不冲突，因为从随机丢弃部分 activation 来实现降低过拟合等价于形成不同的 $V(x)$，从多方向上探索 flat minima，在 test set 上寻找具有更强的模型泛化性的点。在 Dropout 的启发下，形成了最终的 QDrop：

$$QDrop: u = \begin{cases} 0, & \text{with probability } p \\ \hat{a} / a - 1, & \text{with probability } 1 - p \end{cases} \tag{2.15}$$

如 (2.15) 所示，QDrop 以概率 $p$ 丢弃 activation，不进行量化，而以概率 $1 - p$ 对 activation 进行量化。注意，QDrop 和 Case3 不同，QDrop 是在 element-wise 发挥作用的。最终选择的 $p = 0.5$，因此在 $p = 0.5$ 时减少过拟合现象最明显，也具有最大的熵。

QDrop整体流程

图 2.4： QDrop总体流程

从图2.4中可以看出，QDrop并没有对量化主体方法进行改变，因此QDrop可以实现即插即用。

3. 实验现象

图3.1 (a)： QDrop消融

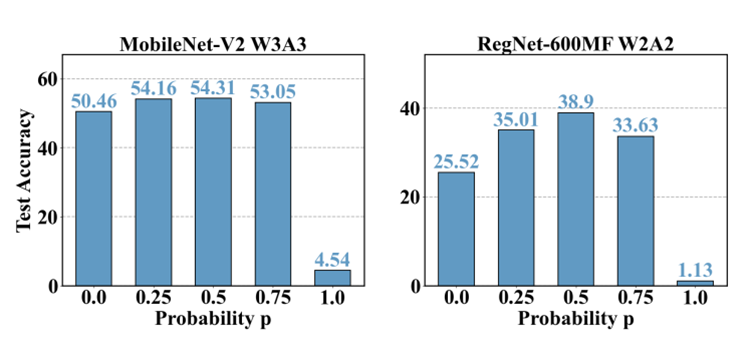
图3.1 (b)： 概率$p$消融

作者首先进行了两个方面的消融实验。首先，测试去掉QDrop的离线量化效果。使用 ImageNet分类基准，将权重量化为2比特，将activation量化为2/4比特。如图3.1(a)所示，QDrop提高了针对ImageNet上6个模型在不同比特下的准确性。此外，将该方法用于轻量级网络架构时，收益更为明显：MNasNet在W2A4下的增量为2.36%，RegNet-3.2GF W2A2 的增量为12.6%。 接下来还探索了QDrop随机失活的概率 对效果的影响。 的选择空间为 [0,0.25,0.5,0.75,1]。测试的结构包含MobileNetV2和RegNet-600MF。结果如图3.1(b)所示。发现0.5通常在5个候选项中表现最好，这也与信息最大化理论相一致。

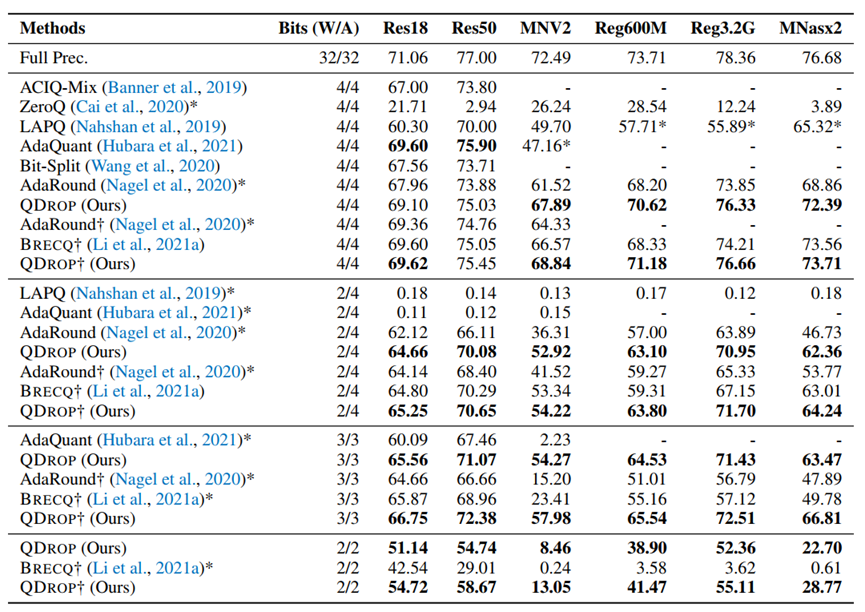
图3.2： ImageNet Benchmark

从图3.2中可以看出，QDrop在低bit的情况下均取得了最好的成绩，尤其是在2W2A情况，成为新的SOTA。

4. 总结分析

再次强调，离线量化PTQ工作的两个难点是：(1)如何获得正确的task loss信息，并使其降低；(2)如何用有限的数据集在短时间内校准出一个量化模型。 QDrop的出现是为了解决第(2)点，首先从将activation noise转化为对应的weight扰动出发，将task loss的二阶优化与flatness挂上钩，并通过随机丢弃activation量化过程实现多方向探索flat minima，以实现用少数有限校正集的前提下使模型在test set上具有更强泛化能力的目的。