AdaRound

传统方法来优化量化是优化的量化参数，即scale和zero point，而AdaRound是从另一种角度来优化，它优化的是四舍五入的量化方式。传统方法中per-tensor的优化空间是2(S和Z)，而AdaRound中采用per tensor的优化空间是N*C*W*H，相比较于传统方法，AdaRound本质上来说相当于扩大了优化空间。通过实验在W4A8 中取得了好的效果。

本人习惯从动机 ->实现技巧 -> 实验的逻辑分析，下面先分析动机。

1. 动机

1.1 从 task loss 剖析

对于量化来说，本质上就是给最初的权重带来一些扰动，优化的意义找到合适的量化参数以减少由量化扰动带来的影响。这种扰动就是由四舍五入带来的，直觉上来说，四舍五入会带来最小的扰动影响，但实际上是这样的吗？

从task loss上来具体分析扰动带来的影响，令$\Delta x$代表扰动，$L\left( {x,y,w} \right)$代表想要最小化的task loss，则扰动对task loss的影响可以用泰勒公式来展开：

$$\tag{1-1} \begin{aligned} E\left[ {L\left( {x,y,w + w} \right) - L\left( {x,y,w} \right)} \right] &\approx E\left[ {{w^T} \cdot {\nabla _w}L\left( {x,y,w} \right) + \frac{1}{2}{w^T} \cdot \nabla _w^2L\left( {x,y,w} \right) \cdot w} \right]\\ &= {w^T} \cdot {g^{\left( w \right)}} + \frac{1}{2}{w^T} \cdot {H^{\left( w \right)}} \cdot w \end{aligned}$$

泰勒只展开到二阶，${g^{\left( w \right)}}$代表task loss对权重w的梯度的期望，${H^{\left( w \right)}}$代表task loss对权重w的Hessian矩阵。

由于原始模型一般是收敛的，${g^{\left( w \right)}}$可近似为0，因此可变为：

$$\tag{1-2} E\left[ {L\left( {x,y,w + \Delta w} \right) - L\left( {x,y,w} \right)} \right] \approx \frac{1}{2}{{\Delta w}^T} \cdot {H^{\left( w \right)}} \cdot \Delta w$$

公式(1.2)将扰动对task loss的影响化简为求Hessian矩阵，为了简便，论文使用了一个toy exampple进行说明。假设${w^T} = \left[ {\Delta {w_1},\Delta {w_2}} \right]$,

$$H^{(w)} =\left [ \begin{matrix}1 & 0.5\\ 0.5&1 \end{matrix} \right ]$$

将其代入(1.2)后为：

$$\tag{1-3} E\left[ {L\left( {x,y,w + \Delta w} \right) - L\left( {x,y,w} \right)} \right] = {\Delta w_1}^2 +{\Delta w_2} ^2 + {\Delta w_1}{\Delta w_2}$$

从公式(1-3)中可以看出，如果采用四舍五入的扰动方式，则只是将${\Delta w_1}^2 +{\Delta w_2} ^2$最小化，并未考虑${\Delta w_1}{\Delta w_2}$，因此四舍五入并非是最优的量化方式。

这是论文里的证明思路，其是从toy example出发，从toy example的发现推广到全局，但这种方式有点类似于先有的剑后有的靶，难以说服。

1.2 设计实验验证动机

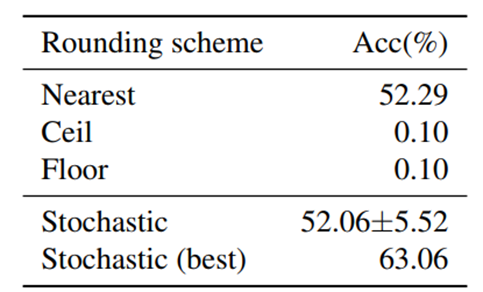
图 1.1： 在ResNet18第一层卷积上量化到4bit的舍入方式对比

从图1.1中可以看出，单纯的向上取整或者向下取整的结果非常差，只有0.1%，四舍五入结果是52.29%，而随机取整虽然波动很大，但是其最优结果可以达到63.06%，超过四舍五入方法近10个点，这初步说明了四舍五入不是最优的舍入方式。

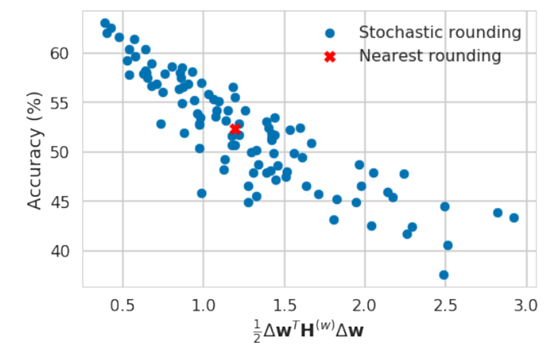
图 1.2： 公式(1.2)与Accuracy的相关性

图1.2展示了式(1.2)与Accuracy的相关性图，从中可以看出，(1.2)与Accuracy呈负相关关系，也说明式(1.2)中的$\frac{1}{2}{{\Delta w}^T} \cdot {H^{\left( w \right)}} \cdot \Delta w$可以替换task loss的波动情形，即式(1.2)是成立的，同样说明用$\frac{1}{2}{{\Delta w}^T} \cdot {H^{\left( w \right)}} \cdot \Delta w$来成为优化目标也是可以的。

2. 实现技巧

2.1 from task loss to QUBO

给定一个已经训练好的预训练模型，我们的目标是最小化由量化带来的task loss的损失，假设使用的是per tensor的对称量化，第层中第个权重量化后在反量化的权重为$\widehat w_i^{\left( l \right)}$，则：

$$\tag{2-1} \widehat w_i^{\left( l \right)} \in \left\{ {w_i^{\left( l \right),floor},w_i^{\left( l \right),ceil}} \right\}$$

其中，$w_i^{\left( l \right),floor} = {s^{\left( l \right)}} \cdot clip\left( {\left\lfloor {\frac{{w_i^{\left( l \right)}}}{{{s^{\left( l \right)}}}}} \right\rfloor ,n,p} \right)$，$[w_i^{\left( l \right),ceil} = {s^{\left( l \right)}} \cdot clip\left( {\left\lceil {\frac{{w_i^{\left( l \right)}}}{{{s^{\left( l \right)}}}}} \right\rceil ,n,p} \right)$，$\left\lfloor \cdot \right\rfloor$代表向下取整，$\left\lceil \cdot \right\rceil$代表向上取整。无论我们怎么优化，只有这两种优化方式。

借鉴1.1小节中的内容，优化最小扰动的过程可以转为：

$$\tag{2-2} \begin{aligned} \mathop {\arg \min }\limits_{w} E\left[ {L\left( {x,y,w + \Delta w} \right) - L\left( {x,y,w} \right)} \right]= \mathop {\arg \min }\limits_{w} E\left[ {{{\Delta w}^{\left( l \right)}}^{^T} \cdot {H^{({w^{^{\left( l \right)}}})}} \cdot {{\Delta w}^{^{\left( l \right)}}}} \right] \end{aligned}$$

(2-2)与(1-2)的区别在于，(2-2)中假设对权重w的Hessian矩阵为块对角阵，即不同层之间的权重互不影响。

由于$\widehat w_i^{\left( l \right)}$只有两种取值方式，因此实现了将task loss转化为了QUBO(二元无约束的优化，Quadratic Unconstrained Binary Optimization)问题。

但是(2-2)仍然面临两大问题：

1. 求解${H^{({w^{^{\left( l \right)}}})}}$仍然极为复杂，难以计算；

2. (2-2)是个NP难问题，不能求解，只能通过穷举法得出结果。

为了解决上述两个问题，需要将QUBO问题进一步转化。

2.2 from QUBO to local loss

这部分是为了解决2.1小节中的第一个问题，即求解${H^{({w^{^{\left( l \right)}}})}}$仍然极为复杂，难以计算。针对这一问题，我们可以通过将原始问题进行化简，解决不掉就绕着走。

对于全连接层，计算第层中某两个权重的二阶导有：

$$\tag{2-3} \begin{aligned} \frac{{{\partial ^2}L}}{{\partial W_{i,j}^{\left( l \right)}\partial W_{m,o}^{\left( l \right)}}} &= \frac{{{\partial ^2}}}{{\partial W_{m,o}^{\left( l \right)}}}\left[ {\frac{{\partial L}}{{\partial z_i^{\left( l \right)}}} \cdot \frac{{\partial z_i^{\left( l \right)}}}{{\partial W_{i,j}^{\left( l \right)}}}} \right]\\ &= \frac{\partial }{{\partial W_{m,o}^{\left( l \right)}}}\left[ {\frac{{\partial L}}{{\partial z_i^{\left( l \right)}}} \cdot x_j^{\left( {l - 1} \right)}} \right]\\ &= \frac{\partial }{{\partial z_m^{\left( l \right)}}}\left[ {\frac{{\partial L}}{{\partial z_i^{\left( l \right)}}}} \right] \cdot \frac{{\partial z_m^{\left( l \right)}}}{{\partial W_{m,o}^{\left( l \right)}}} \cdot x_j^{\left( {l - 1} \right)}\\ &= \frac{{{\partial ^2}L}}{{\partial z_i^{\left( l \right)}\partial z_m^{\left( l \right)}}} \cdot x_j^{\left( {l - 1} \right)} \cdot x_o^{\left( {l - 1} \right)} \end{aligned}$$

其中${z^{\left( l \right)}} = {W^{\left( l \right)}}{x^{\left( {l - 1} \right)}}$是pre-activation，则第层的Hessian矩阵为：

$$\tag{2-4} {H^{({w^{\left( l \right)}})}} = E\left[ {{x^{\left( {l - 1} \right)}} \cdot {x^{{{\left( {l - 1} \right)}^T}}} \otimes \nabla _{{z^{\left( l \right)}}}^2L} \right]$$

其中$\otimes$代表Kronecker积，$\nabla _{{z^{\left( l \right)}}}^2L$代表task loss对pre-activation的Hessian矩阵。可以看出，式(2-4)的意义在于，它将task loss对权重的Hessian矩阵转化为求task loss对pre-activation的Hessian矩阵。但是如果网络层数过深，则会反向求导计算量复杂，求$\nabla _{{z^{\left( l \right)}}}^2L$复杂。

到这里，论文为了再次化简Hessian矩阵，作者提出了又一假设：是对角矩阵且$\nabla _{{z^{\left( l \right)}}}^2{L_{i,i}} = {c_i}$。在这一假设下，有：

$$\tag{2-5} {H^{({w^{\left( l \right)}})}} = E\left[ {{x^{\left( {l - 1} \right)}} \cdot {x^{{{\left( {l - 1} \right)}^T}}} \otimes diag\left( {\nabla _{{z^{\left( l \right)}}}^2{L_{i,i}}} \right)} \right]$$

把式(2.5)代入(2.2)可得：

$$\tag{2-6} \begin{aligned} &\mathop {\arg \min }\limits_{W_{k,:}^{\left( l \right)}} E\left[ {\nabla _{{z^{\left( l \right)}}}^2{L_{k,k}} \cdot \Delta W_{k,:}^{\left( l \right)}{x^{\left( {l - 1} \right)}}{x^{{{\left( {l - 1} \right)}^T}}}\Delta W_{k,:}^{{{\left( l \right)}^T}}} \right] \\ &= \mathop {\arg \min }\limits_{W_{k,:}^{\left( l \right)}} \Delta W_{k,:}^{\left( l \right)}E\left[ {{x^{\left( {l - 1} \right)}}{x^{{{\left( {l - 1} \right)}^T}}}} \right]\Delta W_{k,:}^{{{\left( l \right)}^T}}\\ &= \mathop {\arg \min }\limits_{W_{k,:}^{\left( l \right)}} E\left[ {{{\left( {\Delta W_{k,:}^{\left( l \right)}{x^{\left( {l - 1} \right)}}} \right)}^2}} \right] \end{aligned}$$

式(2.6)的最终表达式就是local loss，而local loss其实在DFQ中的bias correction中已经提出过，优化目标就是每层输出的量化损失，但是在bias correction中的优化对象是量化参数，而local loss是优化的round函数。

2.3 from local loss to AdaRound

上面local loss部分解决了Hessian矩阵难计算和存储的问题，这部分是为了解决2.1小节中的第二问题，即(2.2)是个NP难问题，不能求解，只能通过穷举法得出结果。解决这个问题的核心思想是：既然离散空间难以优化，不如将离散空间的优化问题转化为连续空间的优化，在连续空间中应用之前所学的SGD、Adam等优化算法来解决。

如何将离散空间松弛成连续空间？首先要做的就是转化变量，我们需要一个新的可学习的连续变量，虽然新的变量是连续的，但由于原始变量为二值离散变量，所以新的变量的最终学习目标是成为固定的值。因此新变量的选择要满足两个要求：一是可学习，二是最终取值为固定的值。

论文提出的AdaRound最终采用的方法是：

$$\tag{2-7} \mathop {\arg \min }\limits_V \left\| {Wx - \widetilde Wx} \right\|_F^2 + \lambda {f_{reg}}\left( V \right)$$

其中：

$$\tag{2-8} \widetilde W = s \cdot clip\left( {\left\lfloor {\frac{W}{s}} \right\rfloor + h\left( V \right),n,p} \right)$$ $$\tag{2-9} h\left( {{V_{i,j}}} \right) = clip\left( {\sigma \left( {{V_{i,j}}} \right)\left( {\xi - \gamma } \right) + \gamma ,0,1} \right)$$ $$\tag{2-10} {f_{reg}}\left( V \right) = \sum\limits_{i,j} {1 - {{\left| {2h\left( {{V_{i,j}}} \right) - 1} \right|}^\beta }}$$

其中，$\sigma \left( \cdot \right)$是sigmoid函数，$\xi$为1.1，$\gamma$为-0.1，$\beta$为可变常数。

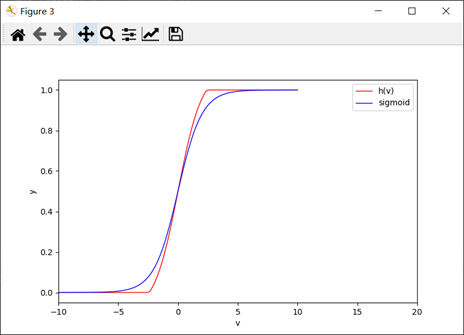
图 2.1： h(V)函数与sigmoid函数图形对比图

从式(2.8)可以看出，AdaRound是将所有round改为下取整，之后再通过$\left[ {0,1} \right]$加上一个取值范围为的连续函数$h\left ( V \right )$来进行调整。由于量化只有上下取整两种方式，所以$h\left ( V \right )$的最终取值只能为0或1，取值为0时对应下取整，取值为1时对应上取整。

为了$h\left ( V \right )$满足的第一个要求：可学习，变量在学习过程中要尽量避免梯度消失的现象，AdaRound采取的$h\left ( V \right )$选取策略如式所示，其实此函数就是Sigmoid函数的变体，其与Sigmoid函数的对比图如图2.1所示，AdaRound中$h\left ( V \right )$就是在Sigmoid的基础上增大了其值域在之间的自变量斜率，以达到避免梯度消失的效果。(是否选取ReLU也可以？)

为了$h\left ( V \right )$满足的第二个要求：最终取值为固定的值(在AdaRound中的$h\left ( V \right )$最终取值只能为0或1)，AdaRound为最终优化目标添加了正则项$\lambda {f_{reg}}\left( V \right)$，利用正则项来控制变量V，使得$h\left ( V \right )$的最终取值只能为0或1，又由于优化函数是求min，这就要求${f_{reg}}\left( V \right)$在为0或者1时取得函数值0。AdaRound采取的策略如式(2-10)所示，函数图如图2.2所示，不同的$\beta$值对应着不同的曲线。至此AdaRound的优化目标构建完毕。

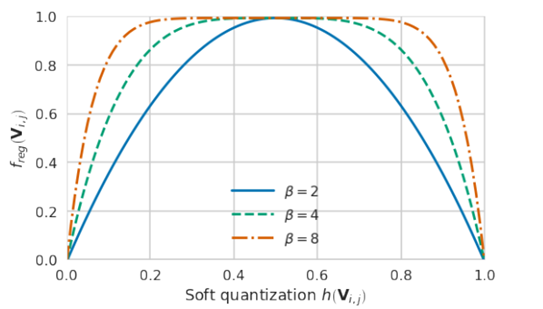
图 2.2： 函数图

2.4 AdaRound如何工作

下面来分析一下式(2-7)是具体是如何起作用的。

首先，对于第一部分$\left\| {Wx - \widetilde Wx} \right\|_F^2$，这部分函数就是在最小化量化损失，相比原本的目标函数，我们把$\widetilde W$中的round函数松弛成连续的情况，这样可以更加方便优化。

之后通过正则项，限制自变量$V$，使得$f(V)$的最终取值只能为0或1，从而实现上取整或者下取整，相当于间接实现了优化local loss的目标。

有一点需要注意，在优化的过程中，$\beta$的值需要逐渐从大到小。这是因为，在初期，有大的$\beta$值，$\lambda {f_{reg}}\left( V \right)$函数有一大段是平谷，且梯度较小，此时loss的降低更多依靠的是量化误差$\left\| {Wx - \widetilde Wx} \right\|_F^2$，可以相对“自由的”往两边跑，从而实现“Adaptive”，而在后期，有小的$\beta$值，$\lambda {f_{reg}}\left( V \right)$函数相对比较陡峭，这时，那些数值小于0.5的$h(V)$就会往左边0的位置收敛，反之，则往右边1的位置靠拢。当$h(V)$的数值为0或者1时候，由图2.1的图像可知，此时梯度为0，$h(V)$也就不会再变动，固定为0或1，进而实现了上下取整。

在优化整个网络的过程中，AdaRound是逐层优化的，先优化第L-1层，再优化第L层，直到优化完所有的层，这样做的好处是在优化第L层时，会充分考虑到前L-1层由量化引起的误差。为了防止激活函数对量化产生影响，论文建议在优化时加入激活函数：

$$\tag{2-11} \mathop {\arg \min }\limits_V \left\| {f\left( {Wx} \right) - f\left( {\widetilde Wx} \right)} \right\|_F^2 + \lambda {f_{reg}}\left( V \right)$$

其中，$f(\cdot)$为激活函数。式2-11即为AdaRound的最终优化函数。

3. 实验现象

注意，AdaRound是属于PTQ的，但它仍然需要一小部分数据集做优化训练(训练round的过程)。论文的所用的优化器为Adam，优化数据集为1024张来自ImageNet的无标签数据，ResNet18上单1080Ti训练所需时间仅为10分钟。

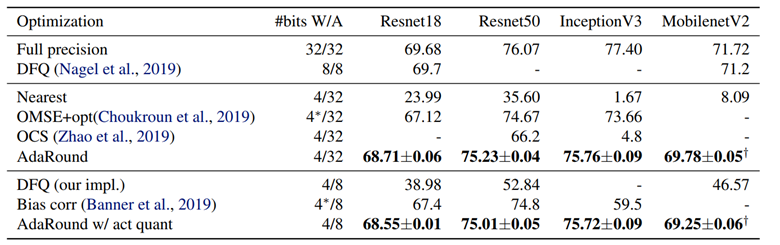
图 3.1： 结果对比

4. 分析

AdaRound从一种新的视角来优化量化误差，这其实是相当于扩大了优化空间，传统方法中per tensor的优化空间是2(S和Z)，而AdaRound中采用per tensor的优化空间是N*C*W*H。按照这个思路的话，其实往下的改进方向也很容易想象，如将优化空间扩大到整个网络，或者某几个layer组成的block，这也就BRQCQ的出发点。