
2024-12-10 | Quantization, BRECQ
经典量化文章阅读——BRECQ
Ctianyang
BRECQ技术分析
BRECQ
这篇文章和AdaRound有很多相同之处,它们都是在对由量化引起的task loss的误差的二阶分析上展开的,并且它对AdaRound中对Hessian矩阵估计的不足之处进行弥补。这篇文章的中心是:在cross layer dependency和泛化误差之间取得balance。因此它侧重于对优化粒度的选择。它也是首篇在W2A4上掉点不严重的文章。
这篇文章依从动机 ->实现技巧 -> 实验的逻辑分析,下面先分析动机。
1. 动机
在引入动机之前,首先要介绍一下本文出现的概念:cross layer dependency,也就是层间依赖关系,作者就是在对cross layer dependency的分析中得出了优化粒度选择的结论。
作者没有直接对cross layer dependency进行解释,我的理解是:cross layer dependency就是不同卷积层的参数之间的互相关联共同影响模型的输出的一种性质。
在AdaRound中,作者为了计算简便,在估计task loss对weights的Hessian矩阵时,做了一个假设:此Hessian是层对角矩阵。这个假设意味着神经网络的各层之间是相互独立的,这就揭示了AdaRound忽视了cross layer dependency,在估计Hessian矩阵时只考虑了层内的依赖性。
也正是AdaRound上述的缺点,导致了AdaRound在INT2量化时掉点严重,因为量化到INT2时,由于量化引起的权重误差会变大,导致泰勒展开时对Hessian矩阵需要更精确的估计,忽视cross layer dependency在此时行不通。作者基于此点想要设计出兼顾cross layer dependency的方法,这就是动机。
2. 实现技巧
2.1 兼顾cross layer dependency
在AdaRound分析过的优化task loss的目标为:
令网络的输出为 ,其中 为网络的权重参数,task loss 用 表示,Hessian 可以通过式 (2.2) 计算:
和 AdaRound 相同,由于预训练模型已经接近收敛,(2.2) 第一项中的 ,因此
记网络输出对权重的雅可比矩阵为 ,因此 Hessian 矩阵可以写成:
(2.4) 完成了将 Hessian 矩阵的计算转化为对雅可比矩阵的计算,然而 仍然是难以存储的,仍然需要对 (2.4) 进行转化。
将由于量化造成的网络输出记为,则有:
将 (2.4) 代入 (2.1) 并结合 (2.5) 可得:
至此,(2.6) 完成了将 task loss 的误差优化问题转化为求对网络的输出 的 Hessian 矩阵。这里有点类似于知识蒸馏。
在知识蒸馏,用一个已经训练好的 Teacher 模型去指导一个初始化的 Student 模型,则让 Student 的输出去学习 Teacher 的输出,这其实也是对网络的输出重建。因此 (2.6) 同样解释了为什么知识蒸馏能够起作用,本质同样都是通过对输出重建来实现对 task loss 的控制。
2.2 对cross layer dependency和泛化误差的再审视
2.1小节中从理论上证明了直接对网络的最终输出进行重建可以很好的对task loss的二阶误差进行估计。但是通过实验,这种方法的结果并没有提高量化的准确率,相反,其使得量化的精度反而下降了。在这种情况下,再度对cross layer dependency进行审视。
在知识蒸馏中,可以用整个数据集来对网络进行优化,而在PTQ中,只有验证集中的几百张数据。因此在PTQ中,直接对网络的输出进行重建容易造成过拟合现象,降低了网络的泛化能力。 而AdaRound中的对layer进行重建的方法相比于对网络的最终输出进行重建,逐层重建要求量化模型的每一层输出都强制与全精度模型尽可以相似,这就相当于引入了逐层正则项,通过添加正则项来对网络优化进行限制,这也是相对地增加了网络的泛化能力。
BRECQ通过分析,逐层重建忽略了cross layer dependency,但是却有较强的泛化能力;而对网络的最终输出进行重建加强了cross layer dependency,但是泛化能力差。是否存在一种存在于层和网络输出之间的中间粒度能够在cross layer dependency和泛化能力之间取得balance呢?这就是2.3小节选择优化粒度的动机所在,这是作者通过在实验的过程中所启发而来。
其实在AdaRound中也可以由另一角度得到相同的灵感。AdaRound既希望能够尽可能的保留task loss的整网信息,却又到最后推导到了逐层优化,但逐层优化显然又丢失了层间信息。从这角度也能想到粒度选择的问题。
2.3 选择优化粒度
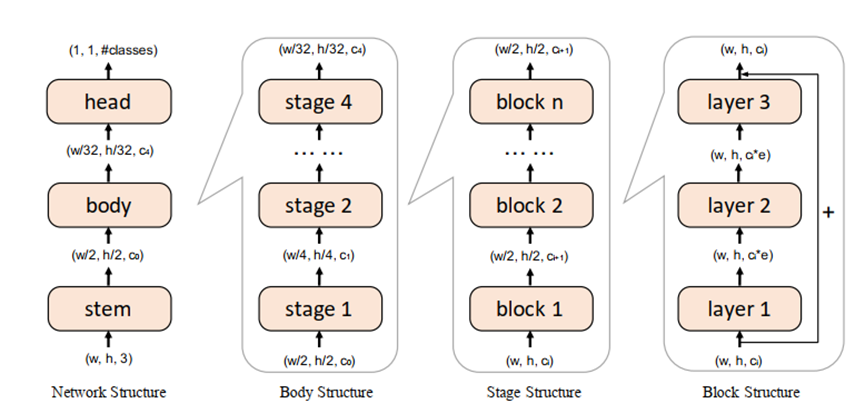
图 2.1: Layer、Block、Stage、Network的定义示例
如图2.1所示,在选择优化粒度时作者借鉴了ResNet网络中对结构的划分机制将网络划分为四部分:Layer、Block、Stage、Network。
Layer-wise Reconstruction:和AdaRound中的做法相同;
Block-wise Reconstruction:例如ResNet中的Residual Block,在此方法中认为Hessian矩阵是Block对角矩阵,并重建Block的输出,按顺序进行优化;
Stage-wise Reconstruction:Stage的分界点就是网络输入要被下采样和增加通道数的节点,在此方法中认为Hessian矩阵是Stage对角矩阵,并重建Stage的输出,按顺序进行优化;
Network-wise Reconstruction:这也就是2.1小节中对网络输出进行重建的方法,类似于知识蒸馏,但并没取得好结果。
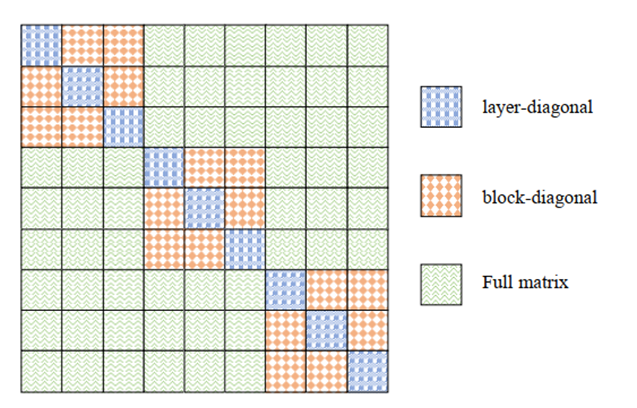
图 2.2: Hessian矩阵示意图
在图2.2中解释了由Hessian反映出的cross layer dependency,蓝色部分表示Hessian矩阵的估计为层对角矩阵,在这里只考虑了层内的依赖关系,忽视了层间的依赖关系。橙色部分表示Hessian矩阵的估计为Block对角矩阵,在这里只考虑了Block内的依赖关系,忽视了Block间的依赖关系。
但是在构建优化粒度中,作者并没有给出最优方案,仅仅按照直觉划分为了四个维度,Block的定义没有做到通用,由此点可以继续往下进行研究。
2.4 对pre-activation的Hessian矩阵的估计处理
在 AdaRound中,作者先通过 Hessian 矩阵按 Layer 对角矩推导了逐层构建的方式:
接下来在对 pre-activation 计算 Hessian 又做了一个假设:, 即 pre-activation 的 Hessian 矩阵与输入数据无关是一个常数,因此二阶误差优化也就成为了:,即直接对层的输出重建,并通过消融实验展示在 W4A8 中此假设的合理性设不会给结果造成精度下降。
然后在W2A4 中,AdaRound却有明显的精度下降。本质原因在第1小节的动机部分阐述过,在W2A4中由于量化引起的权重误差 会变大,导致泰勒展开到二阶时对Hessian矩阵需要更精确的估计。
为了在AdaRound的基础上强化对pre-activation计算Hessian的信息,作者选择了用Fisher Information矩阵(FIM)来估计Hessian矩阵。这是因为FIM本身和Hessian矩阵就有联系:FIM是对数似然函数的Hessian矩阵的负期望,用数学表示为:
为了在 AdaRound 的基础上强化对 pre-activation 计算 Hessian 的信息,作者选择了用 Fisher Information 矩阵 (FIM) 来估计 Hessian 矩阵。这是因为 FIM 本身和 Hessian 矩阵就有联系: FIM 是对数似然函数的 Hessian 矩阵的负期望,用数学表示为:
(2.8) 揭示了一个很重要的原理:当 task loss 是 (输出是连续分布或者交叉熵(输出是离散分布)时,可用 FIM 来估计 Hessian 矩阵。 更本质来讲,如果我们模型的输出分布和真实的数据分布相近时,可用 FIM 来估计 Hessian 矩阵。
因此作者采用 FIM 来估计 Hessian 时,也做了一个大胆的假设:模型输出分布和数据真实分布相近。但这在量化中是可行的,因为量化前的预训练模型已经收敛。对 pre-activation 的 FIM 的对角元素等于各元素梯度的平方(KFAC 中已证明),因此优化目标为:
与直接令Hessian矩阵的对角为常数而得出的MSE相比,用FIM估计Hessian矩阵得出的优化目标(2.9)中包含了平方梯度的信息。
2.5 整体流程
2.1-2.4小节为BRECQ的核心算法推演部分,作者选择了Block作为优化粒度,并将优化目标由AdaRound的layer wise的MSE进一步推演为(2.9)。同样,作者在对权重量化时借鉴了AdaRound中对round的优化策略,在对激活值量化时借鉴了learned step size策略。

图 2.3: BRECQ算法图
3. 实现技巧
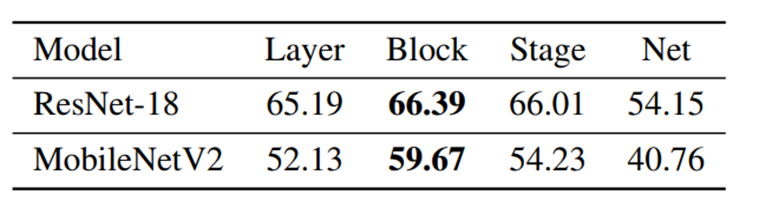
图 3.1: BRECQ算法图
图3.1所示的消融实验表明,在本文的四种优化粒度当中,Block粒度展示出了最好的结果。因此作者选择了Block wise作为最终的优化粒度。
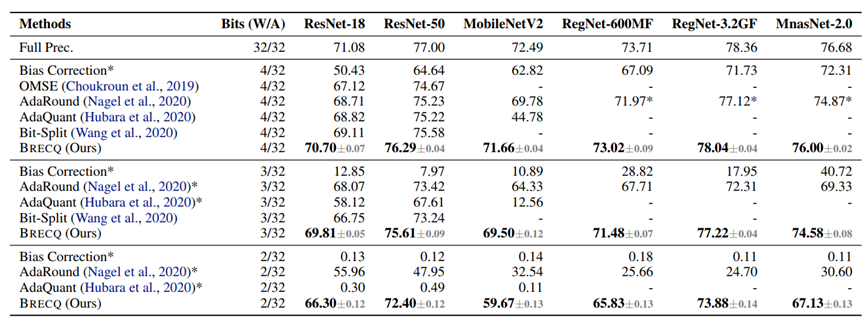
图 3.2(a): 与只量化weight的方法对比
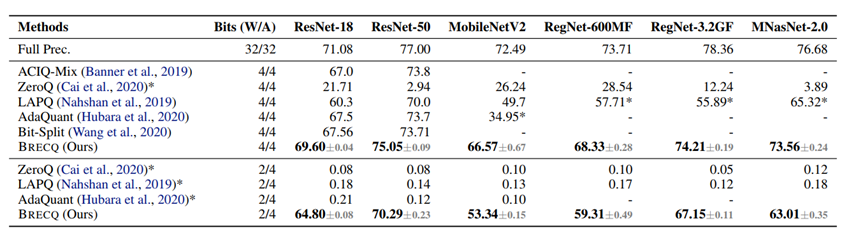
图 3.2(b): 不仅量化weight,也量化activation
图3.2展示了BRECQ与一些经典的PTQ算法对比,结果展示,BRECQ在4bit上领先其他算法,而且首次在2bit展现了可以在工业界使用的精度。
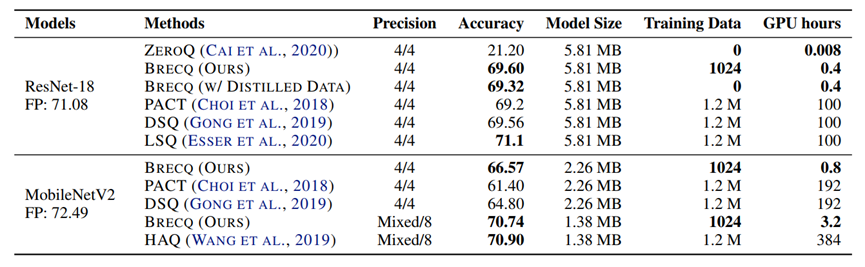
图 3.3: 与QAT算法对比
4. 分析
AdaRound和BRECQ都是运用了优化方法从task loss上作为切入点,而不是直接的量化权重本身的误差,这也是当前量化工作的共同点。
在此基础上,当前PTQ工作的两个难点是:
(1)如何获得正确的task loss信息,并使其降低;
(2)如何用有限的数据集在短时间内校准出一个量化模型。
对于问题(1),AdaRound采用的方法是通过两个强假设:task loss对权重的Hessian矩阵为层对角矩阵且task loss对pre-activation的Hessian矩阵是个主对角线元素均为常数的对角矩阵,将二阶误差优化问题转化为层重建。但是,这两个强假设丢失task loss信息。BRECQ在AdaRound的基础上,通过对cross layer dependency和泛化误差的分析,得出选择优化粒度的结论,选择Block作为基础的优化粒度。本质的目的就是在task loss信息和泛化能力之间取得balance。为了进一步的保留task loss信息,BRECQ在估计task loss对pre-activation的Hessian矩阵时用了FIM来替代Hessian矩阵,相比于AdaRound融入进了一阶梯度信息。
对于问题(2),在BRECQ中也有所提及,在选择整网输出作为重建粒度时,效果并不如预期。这和知识蒸馏十分类似,但是知识蒸馏却能够起作用而在PTQ中不行是因为,PTQ的校准集很少。
